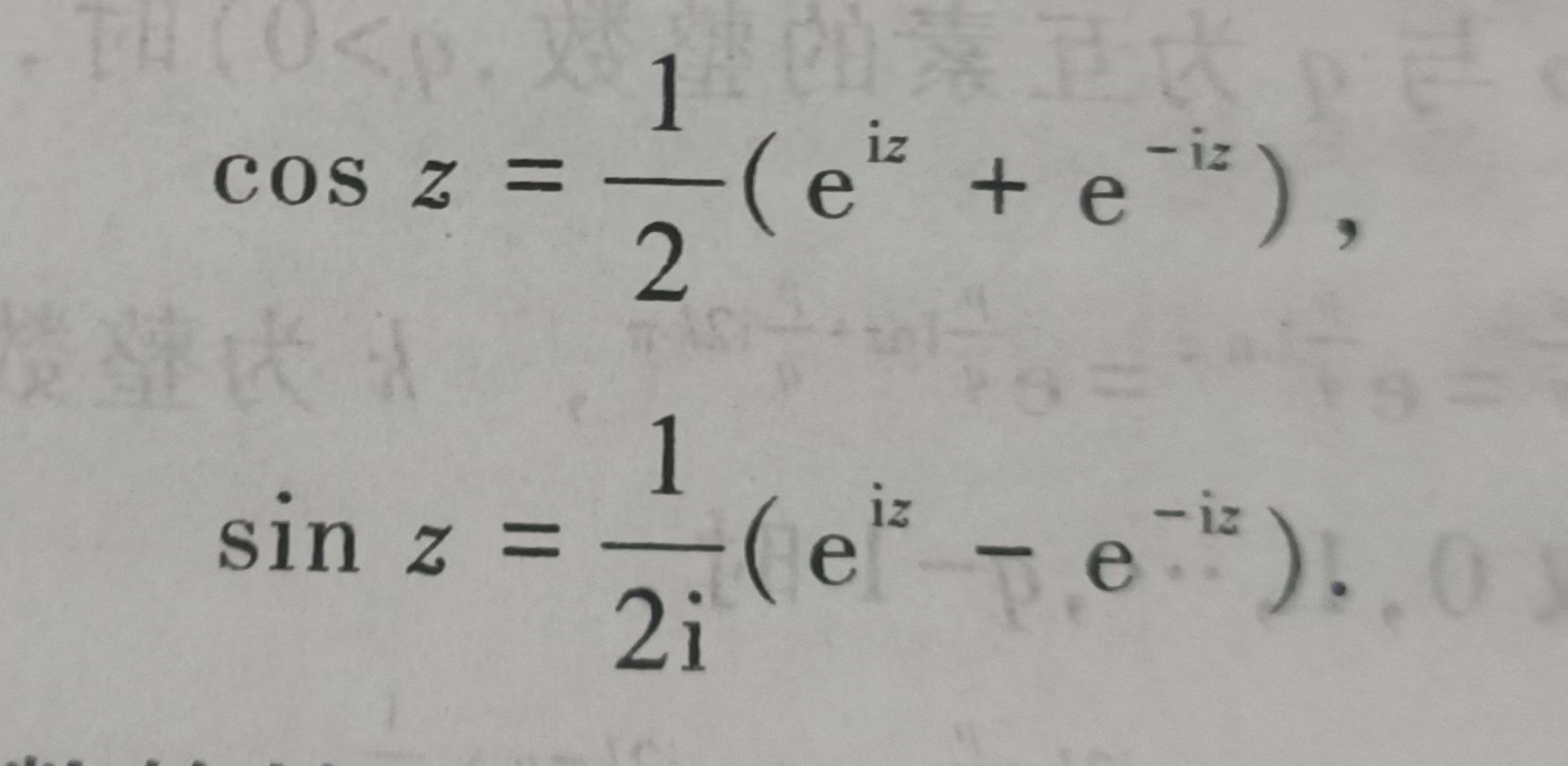复变函数与积分变换
马上就要考试了,悲
复数与复变函数
复数的三种形式
- 复数的一般形式 $Z=x+yi$
- 复数的三角表示 $Z=r(\cos\theta+j\sin\theta)$
- 复数的指数形式 $Z=re^{i\theta}$
复数的主值与辐值
$$ArgZ = argZ + 2k\pi$$
其中 $0 \leq argZ<2\pi$
主值的求解公式
棣莫弗公式 ★
$$Z^n=[r(\cos\theta+i\sin\theta)]^n=r^n(\cos{n\theta}+\sin{n\theta})=re^{in\theta}$$
当r=1时,有
$$(\cos\theta+i\sin\theta)^n=\cos{n\theta}+\sin{n\theta}$$
逆运用
$$w=r^{\frac{1}{n}}[\cos(\frac{1}{n}(\theta+2k\pi))+i\sin(\frac{1}{n}(\theta+2k\pi))]$$
其中$k=0,1,2,…,n-1$
$r=|Z|$
练习
共轭复数
$ReZ=\frac{Z+\overline{Z}}{2}$
$ImZ=\frac{Z-\overline{Z}}{2i}$
解析函数
解析函数:概念性质、充分/必要条件、调和函数、初等函数
解析概念:
$w=f(Z)$如果在$Z_{0}$及其领域内处处可导,则$f(Z)$在$Z_{0}$处解析
解析->可导->连续
反之不行
函数解析的充要条件(柯西-黎曼方程)
C-R方程
$f(z)=u(x,y)+iv(x,y)$在$z=x+iy$处处可导的充要条件是$u(x,y)$,$v(x,y)$在点$(x,y)$处可微
$$\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}且\frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x}$$
调和函数
调和函数和解析函数针对的对象不同
解析函数针对$f(Z)$
调和函数针对$u(x,y)与v(x,y)$
拉普拉斯方程(Laplace)
$$
\frac{\partial^{2} \varphi}{\partial^{2}x}+ \frac{\partial^{2} \varphi}{\partial^{2}y}=0
$$
解析函数的实部和虚部是调和函数
初等函数
指数函数
$$e^{Z}=e^{x+iy}=e^{x}(\cos x +i\sin y)$$
指数函数性质有:
- $ |e^{Z}|=e^{x}$
- $Arg(e^{Z})=y+2k\pi$
- $e^{Z+i2k\pi}=e^{Z},即e^{Z}是以2k\pi 为周期的周期函数$
- $(e^{Z})’=e^{Z}$
对数函数
$LnZ=lnZ+i2k\pi=ln|Z|+iargZ+i2k\pi$
幂函数
$a^{b}=e^{(Lna)b}$
三角函数
反三角函数
练习
复变函数的积分
定义及如何积分
定义在简单光滑或分段光滑上的有向曲线上的积分
$$f(Z)=u(x,y)+iv(x,y)$$
$$f_{c}(Z)dZ$$
如何积分?两种方法
- 第二型曲线积分
$$\int_{c}(Z)dZ=\int_{c}u(x,y)+iv(x,y)dZ=\int_{c}udx-vdy+i\int_{c}vdx+udy$$ - 参数法
$$\int_{c}(Z)dZ=\int^{\beta}_{\alpha}f(Z(t))Z’(t)dt$$
柯西-古萨定理
$$\oint_{c}f(Z)dZ=0$$
$f(Z)$在C上及D内解析则成立
复合闭路定理
推导
$f(Z)$在$\Gamma$上解析,
且$\Gamma=C+C^{-}{1}+C^{-}{2}$+…,
则$\oint_{\Gamma}f(Z)dZ=0$,
代入$\Gamma =C+C^{-}{1}+C^{-}{2}$+…
则$\oint_{C+C^{-}{1}+C^{-}{2}+…}f(Z)dZ=0$ 化简移项可得
$$\oint_{c}f(Z)dZ= \sum_{n=1}^n\oint_{C_{k}}f(Z)dZ$$
当k=1时,则得
$$\oint_{c}f(Z)dZ= \oint_{k}f(Z)dZ$$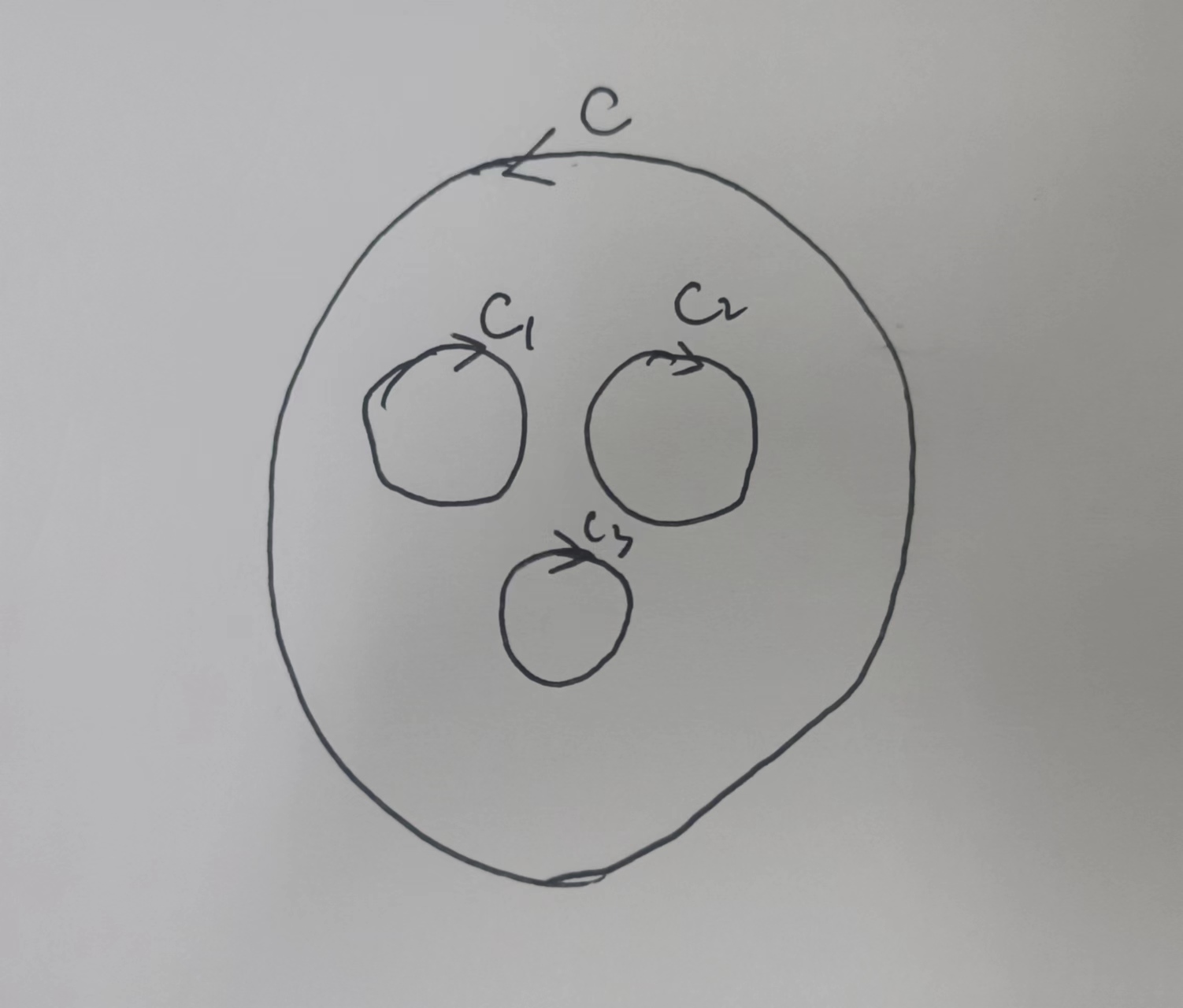
柯西积分公式 ★
适用条件:$f(Z)$要在C上及其内部解析
$$\oint_{c}\frac{f(Z)}{Z-Z_{0}}dZ= 2\pi if(Z_{0})$$
高阶
$$\oint_{c}\frac{f(Z)}{(Z-Z_{0})^{n-1}}dZ= \frac{2\pi i}{n!} f(Z_{0})$$
级数(研究其敛散性)
级数的一些性质
$\sum_{n=1}^n|Z|$收敛,则$\sum_{n=1}^nZ$也收敛
- $\sum_{n=1}^n\frac{1}{n}$是发散的
复数序列
$Z_{1}=a_{1}+b_{1}i$,$Z_{2}=a_{2}+b_{2}i$,…$Z_{n}=a_{n}+b_{n}i$,…
上面的序列,简记为
$${Z_{n}}$$
项级数
如何判断一个项级数是收敛还是发散的呢?部分和判断
部分和为
$$S_{n}=Z_{1}+Z_{2}+…Z_{n}$$
部分和序列$${S_{n}}=S_{1}+S_{2}+…S_{n}$$
幂级数 ★

形式和收敛半径要记住,收敛半径的求法,比值法和根值法。
其级数在其收敛半径内部绝对收敛,在其收敛半径上不一定。
幂级数的运算(加减乘除)
对应题型,将函数展开为Z的幂级数(不熟练)
泰勒级数

洛朗级数
- 求收敛圆环的半径
- 展开为洛朗级数
负幂项的收敛半径按正幂项求,最后取倒数。
留数及其应用
奇点及奇点的分类及求法
- 孤立奇点(洛朗展开仅有正幂项)
- n阶极点(有负幂项,部分为0)
- 本性奇点(洛朗展开既有正幂项,又有负幂项)