Posted on  Updated on 

算法基础-十大排序算法

十大排序算法

  1. 选择排序
  2. 冒泡排序
  3. 插入排序
  4. 希尔排序
  5. 计数排序
  6. 桶排序
  7. 基数排序
  8. 归并排序
  9. 快速排序
  10. 堆排序

1. 时间复杂度（Time Complexity）

时间复杂度 是 衡量算法执行时间增长与输入规模关系的指标。
它描述了 输入规模 ( n ) 变化时，算法执行的基本操作次数。

🔹 常见时间复杂度

时间复杂度 复杂度名称 示例
( O(1) ) 常数时间 直接返回结果 return a + b
( O(\log n) ) 对数时间 二分查找
( O(n) ) 线性时间 遍历数组
( O(n \log n) ) 线性对数时间 归并排序、快速排序
( O(n^2) ) 二次时间 双层嵌套循环（冒泡排序）
( O(2^n) ) 指数时间 递归斐波那契
( O(n!) ) 阶乘时间 旅行商问题（TSP）

🔹 计算时间复杂度

  1. 只关注最大数量级，忽略常数

    1
    2
    for i in range(n):  # O(n)
        print(i)
    • 遍历 ( n ) 次，时间复杂度是 ( O(n) )。

  2. 嵌套循环相乘

    1
    2
    3
    for i in range(n):       # O(n)
        for j in range(n):   # O(n)
            print(i, j)
    • 总共执行 ( n \times n = O(n^2) ) 次。

  3. 对数复杂度 ( O(\log n) )

    1
    2
    3
    i = 1
    while i < n:
        i *= 2
    • i 每次翻倍，循环运行约 ( \log_2 n ) 次，因此复杂度是 ( O(\log n) )。

2. 空间复杂度（Space Complexity）

空间复杂度 是 衡量算法运行时需要占用多少额外的存储空间。

🔹 常见空间复杂度

空间复杂度 说明 示例
( O(1) ) 只使用常数级别的额外存储 交换两个数
( O(n) ) 需要存储 ( n ) 个数据 额外创建数组
( O(n^2) ) 需要存储 ( n \times n ) 矩阵 图的邻接矩阵

🔹 计算空间复杂度

  1. 基本变量（O(1）

    1
    2
    a = 10
    b = 20
    • 只使用了 常数级别的变量，所以是 ( O(1) )。

  2. 数组或列表（O(n）

    1
    arr = [0] * n
    • 额外创建了 ( n ) 个存储单元，复杂度是 ( O(n) )。

  3. 递归（O(n)）

    1
    2
    3
    4
    def factorial(n):
        if n == 0:
            return 1
        return n * factorial(n - 1)
    • 递归调用占用 ( O(n) ) 栈空间。

总结

复杂度类型 时间复杂度 空间复杂度 示例
最优算法 ( O(1) ) ( O(1) ) 直接返回值
一般算法 ( O(n) ) ( O(n) ) 遍历列表
较差算法 ( O(n^2) ) ( O(n^2) ) 矩阵运算
最差算法 ( O(2^n) ) ( O(n) ) 递归斐波那契

💡 目标：尽量优化算法，使时间复杂度和空间复杂度更小！ 🚀

选择排序

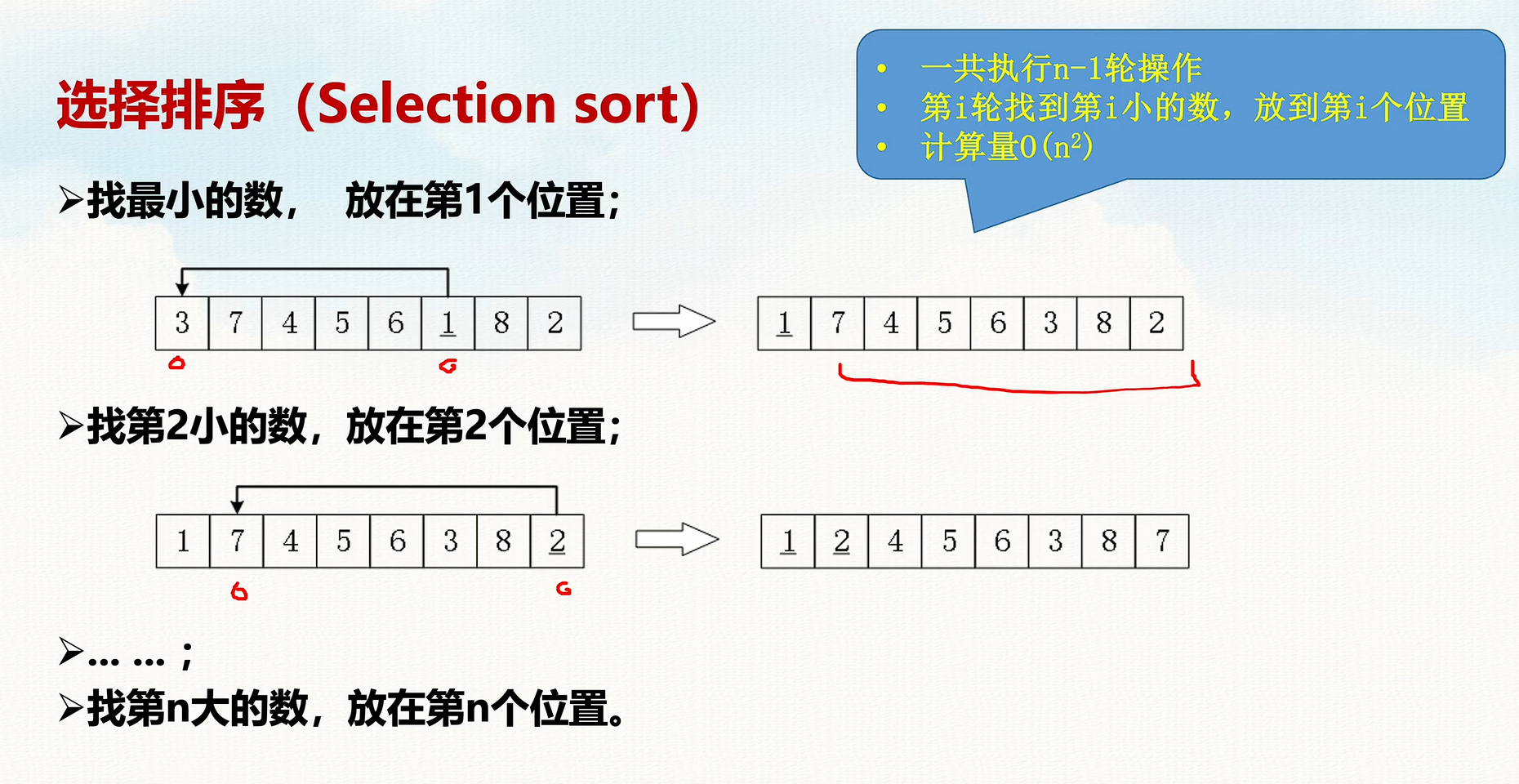
🔹 选择排序原理

  1. 遍历数组，在未排序部分找到最小值；
  2. 交换最小值与当前元素；
  3. 重复步骤 1 和 2，直到整个数组有序。

等同于打擂台排序

🔹 Python 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def selection_sort(arr):
    n = len(arr)
    for i in range(n - 1):  # 遍历每个位置（除了最后一个）
        min_index = i  # 假设当前索引是最小值
        for j in range(i + 1, n):  # 在剩下的部分查找更小的值
            if arr[j] < arr[min_index]:
                min_index = j  # 记录最小值索引

        if min_index != i:  # 如果找到了更小的值，则交换
            arr[i], arr[min_index] = arr[min_index], arr[i]

    return arr

# 测试代码
arr = [64, 25, 12, 22, 11]
sorted_arr = selection_sort(arr)
print("排序后的数组:", sorted_arr)

🔹 运行结果

1
排序后的数组: [11, 12, 22, 25, 64]

🔹 时间复杂度

  • 最佳情况：( O(n^2) )（已经排序仍然需要比较）
  • 最差情况：( O(n^2) )（完全逆序，需要交换）
  • 平均情况：( O(n^2) )

🔹 空间复杂度

  • ( O(1) )（原地排序，无额外空间开销）

✅ 选择排序适用于小规模数据，但对于大数据不够高效 🚀

冒泡排序

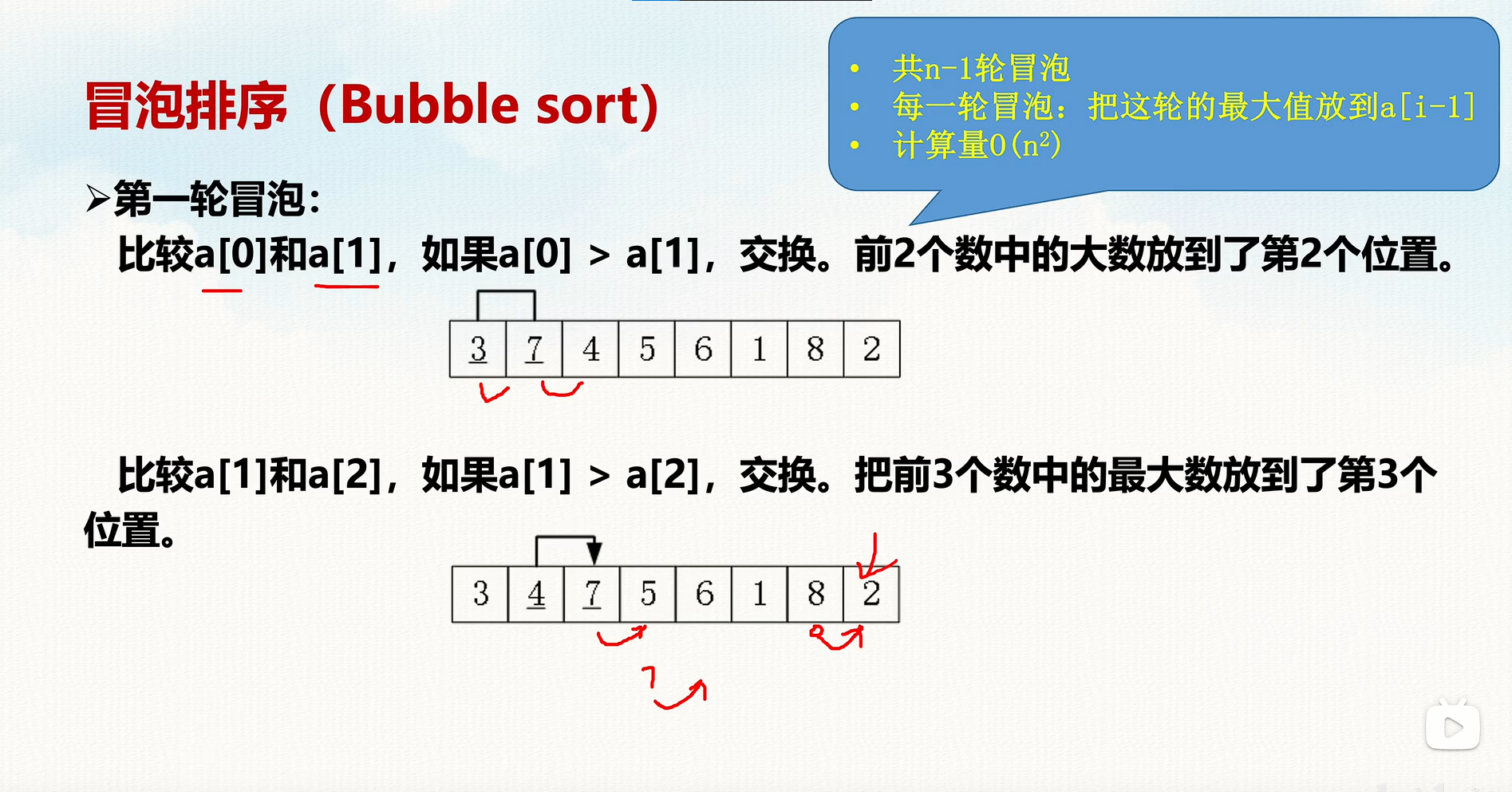
冒泡排序原理：

  1. 两两比较相邻元素，如果顺序不对，则交换它们；
  2. 一轮遍历后，最大元素会被“冒泡”到数组末尾；
  3. 重复步骤 1 和 2，直到整个数组有序。

🔹 Python 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def bubble_sort(arr):
    n = len(arr)
    for i in range(n - 1):  # 总共进行 n-1 轮排序
        swapped = False  # 标记变量，优化性能
        for j in range(n - 1 - i):  # 每轮遍历未排序部分
            if arr[j] > arr[j + 1]:  # 交换相邻元素
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
                swapped = True
        if not swapped:  # 如果没有发生交换，说明已排序好
            break
    return arr

# 测试代码
arr = [64, 25, 12, 22, 11]
sorted_arr = bubble_sort(arr)
print("排序后的数组:", sorted_arr)

🔹 运行结果

1
排序后的数组: [11, 12, 22, 25, 64]

🔹 时间复杂度

  • 最佳情况：( O(n) )（已排序，优化版本只需 1 轮）
  • 最差情况：( O(n^2) )（完全逆序）
  • 平均情况：( O(n^2) )

🔹 空间复杂度

  • ( O(1) )（原地排序，无额外空间）

✅ 适用于小规模数据，但对于大数据效率低 🚀

插入排序

插入排序原理：

  1. 将数组分成 已排序 和 未排序 两部分。
  2. 依次从未排序部分取出元素，插入 到已排序部分的正确位置。
  3. 直到所有元素都插入完成，数组变为有序。

开始有序区只有一个，比他大的都往后移动一个格子

🔹 Python 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def insertion_sort(arr):
    n = len(arr)
    for i in range(1, n):  # 从第二个元素开始（索引 1）
        key = arr[i]  # 取出当前待插入的元素
        j = i - 1
        while j >= 0 and arr[j] > key:  # 向左寻找合适位置
            arr[j + 1] = arr[j]  # 后移元素
            j -= 1
        arr[j + 1] = key  # 插入元素
    return arr

# 测试代码
arr = [64, 25, 12, 22, 11]
sorted_arr = insertion_sort(arr)
print("排序后的数组:", sorted_arr)

🔹 运行结果

1
排序后的数组: [11, 12, 22, 25, 64]

🔹 时间复杂度

  • 最佳情况：( O(n) )（数组已排序）
  • 最差情况：( O(n^2) )（完全逆序）
  • 平均情况：( O(n^2) )

🔹 空间复杂度

  • ( O(1) )（原地排序）

✅ 适用于小规模数据，稳定排序，性能优于冒泡排序 🚀

希尔排序

【数据结构——一分钟搞定插入排序】 https://www.bilibili.com/video/BV1Y8411T7LC/?share_source=copy_web&vd_source=59d9734fc97a6b9510465651bf85b98c

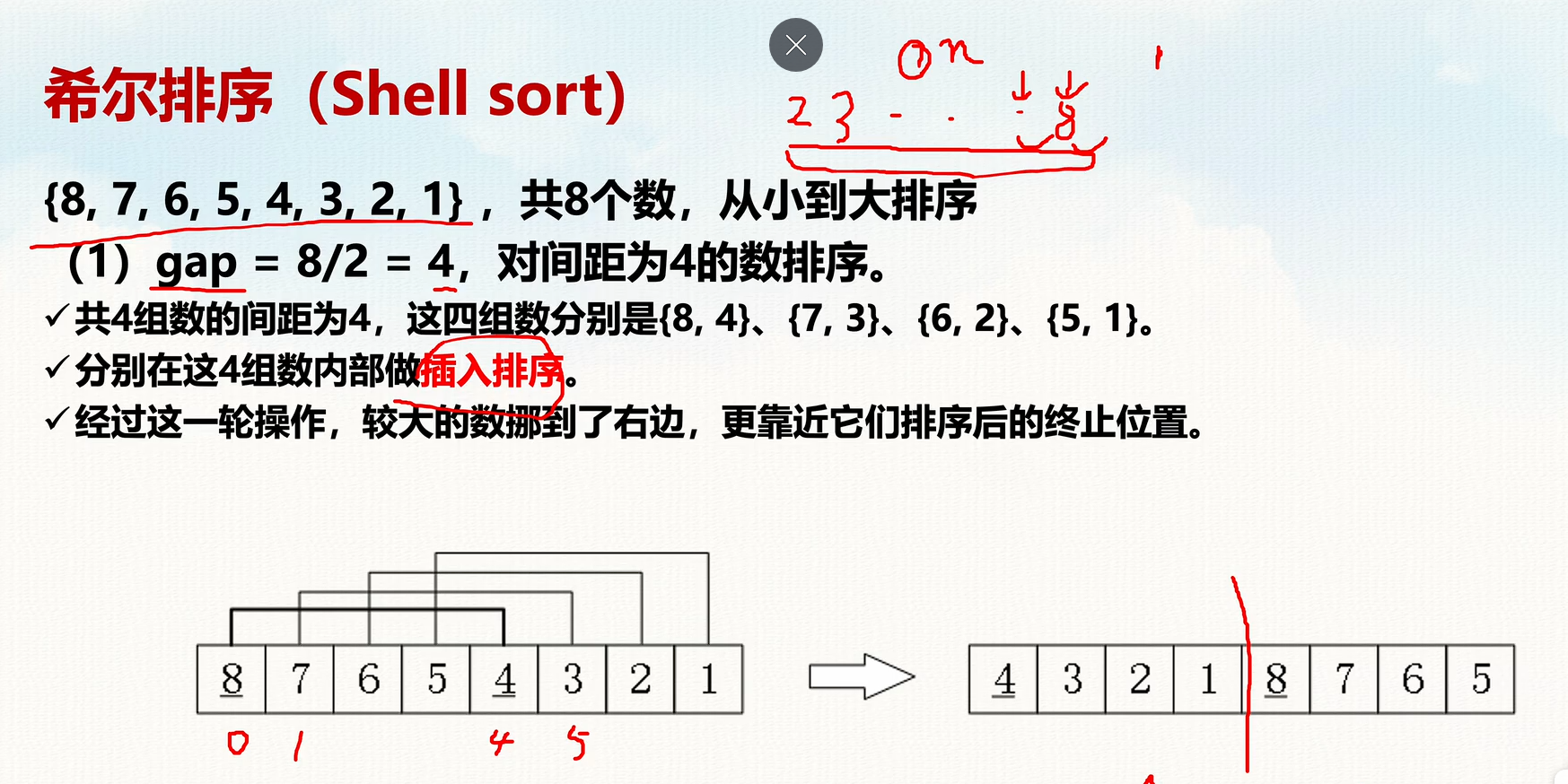
希尔排序原理：

  1. 基于插入排序 的改进版本，先对 较大间隔 的元素进行排序，再逐步减小间隔，最终进行普通插入排序。
  2. 这样可以减少数据移动次数，提高效率。

🔹 Python 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def shell_sort(arr):
    n = len(arr)
    gap = n // 2  # 初始步长

    while gap > 0:
        for i in range(gap, n):
            key = arr[i]
            j = i
            while j >= gap and arr[j - gap] > key:
                arr[j] = arr[j - gap]  # 后移元素
                j -= gap
            arr[j] = key  # 插入元素
        gap //= 2  # 缩小步长
    return arr

# 测试代码
arr = [64, 25, 12, 22, 11]
sorted_arr = shell_sort(arr)
print("排序后的数组:", sorted_arr)

🔹 运行结果

1
排序后的数组: [11, 12, 22, 25, 64]

🔹 时间复杂度

  • 最佳情况：( O(n \log n) )（取决于步长选择）
  • 最差情况：( O(n^2) )（极端情况下）
  • 平均情况：( O(n^{1.3 - 2}) )（根据步长序列不同）

🔹 空间复杂度

  • ( O(1) )（原地排序）

✅ 适用于中等规模数据，比插入排序和冒泡排序更快 🚀

计数排序

🔹 计数排序（Counting Sort）

计数排序原理：

  1. 适用于整数排序，尤其是范围较小的非负整数。
  2. 统计每个元素出现的次数，利用计数数组（桶）进行排序。
  3. 时间复杂度接近 ( O(n) )，但空间复杂度较高。

🔹 Python 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
def counting_sort(arr):
    if not arr:
        return arr

    max_val = max(arr)  # 找到数组中的最大值
    min_val = min(arr)  # 找到数组中的最小值
    range_val = max_val - min_val + 1  # 计算值域大小

    # 创建计数数组并初始化为0
    count = [0] * range_val
    output = [0] * len(arr)

    # 统计元素出现次数
    for num in arr:
        count[num - min_val] += 1

    # 计算前缀和，确定元素在输出数组中的位置
    for i in range(1, len(count)):
        count[i] += count[i - 1]

    # 填充排序后的数组（倒序遍历确保稳定性）
    for num in reversed(arr):
        output[count[num - min_val] - 1] = num
        count[num - min_val] -= 1

    return output

# 测试代码
arr = [4, 2, 2, 8, 3, 3, 1]
sorted_arr = counting_sort(arr)
print("排序后的数组:", sorted_arr)

🔹 运行结果

1
排序后的数组: [1, 2, 2, 3, 3, 4, 8]

🔹 时间复杂度

  • 最佳情况：( O(n + k) )（k 为数值范围）
  • 最差情况：( O(n + k) )
  • 平均情况：( O(n + k) )

🔹 空间复杂度

  • ( O(k) ) + ( O(n) )（需要额外的计数数组）

✅ 适用于整数排序，尤其是数据范围较小、重复率较高的情况 🚀

桶排序

每个桶内部的排序方式多种多样

基数排序

归并排序

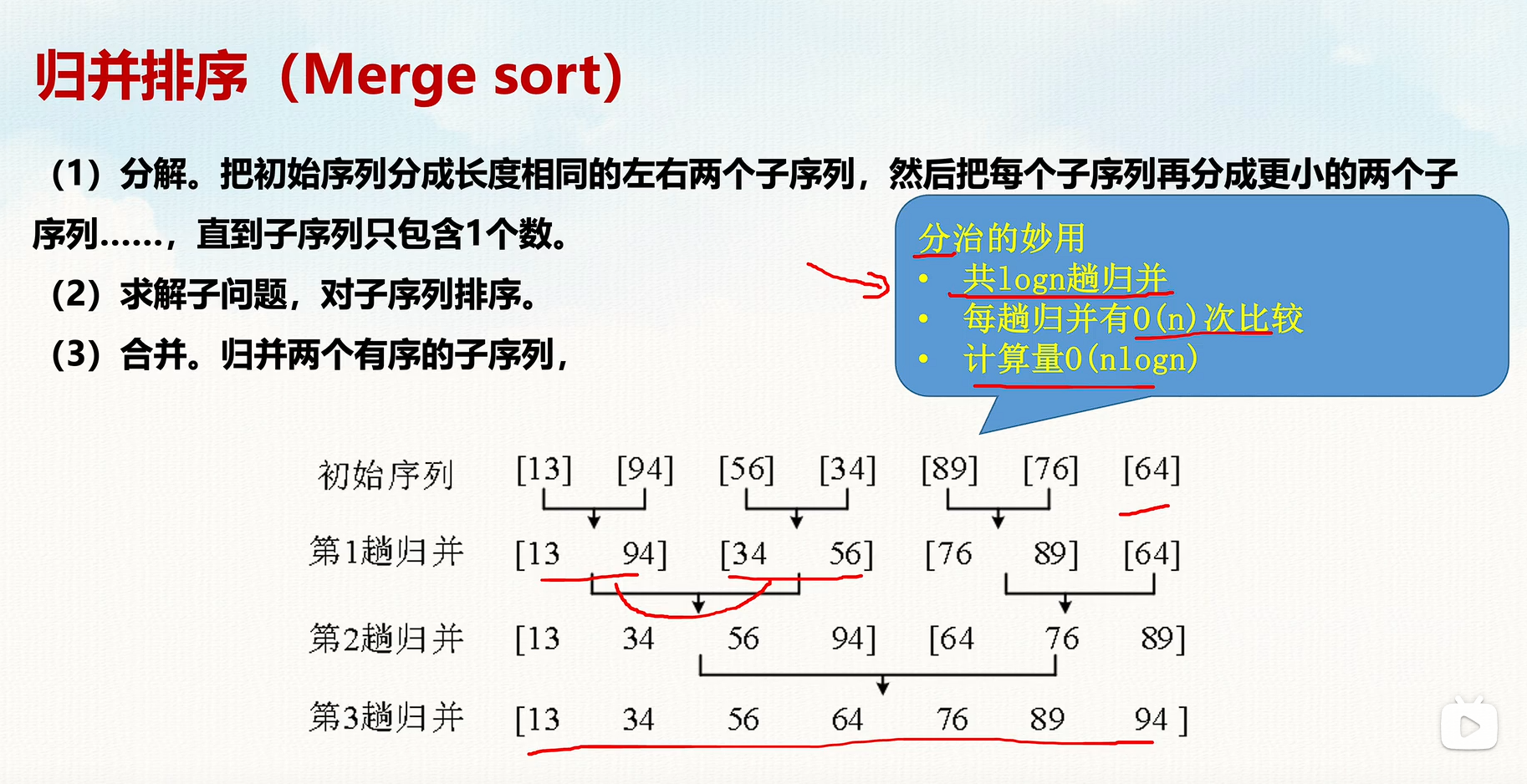
🔹 归并排序（Merge Sort）

归并排序原理：

  1. 分割：将数组递归地分成两半，直到每部分只剩一个元素。
  2. 合并：合并两个有序数组，保持整体有序。
  3. 时间复杂度：( O(n \log n) )，适用于大规模数据排序。

🔹 Python 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
def merge_sort(arr):
    if len(arr) <= 1:  # 递归终止条件
        return arr

    # 1. 分割数组
    mid = len(arr) // 2
    left_half = merge_sort(arr[:mid])  # 递归排序左半部分
    right_half = merge_sort(arr[mid:])  # 递归排序右半部分

    # 2. 合并两个有序数组
    return merge(left_half, right_half)

def merge(left, right):
    sorted_list = []
    i = j = 0  # 左右数组的索引

    # 逐步合并两个有序数组
    while i < len(left) and j < len(right):
        if left[i] < right[j]:
            sorted_list.append(left[i])
            i += 1
        else:
            sorted_list.append(right[j])
            j += 1

    # 处理剩余元素
    sorted_list.extend(left[i:])
    sorted_list.extend(right[j:])
    
    return sorted_list

# 测试代码
arr = [12, 11, 13, 5, 6, 7]
sorted_arr = merge_sort(arr)
print("排序后的数组:", sorted_arr)

🔹 运行结果

1
排序后的数组: [5, 6, 7, 11, 12, 13]

🔹 时间复杂度

  • 最佳情况：( O(n \log n) )
  • 最差情况：( O(n \log n) )
  • 平均情况：( O(n \log n) )

🔹 空间复杂度

  • ( O(n) )（需要额外的存储空间）

✅ 适用于大规模数据排序，尤其是稳定排序需求场景 🚀

快速排序

🔹 快速排序（Quick Sort）

原理：

  1. 选择基准（pivot）：一般选择数组中的一个元素作为基准。
  2. 分区（Partition）：
    • 小于基准的放左边，
    • 大于基准的放右边。
  3. 递归处理：分别对左、右子数组递归执行快速排序，直到数组有序。

🔹 Python 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def quick_sort(arr):
    if len(arr) <= 1:  # 递归终止条件
        return arr

    pivot = arr[len(arr) // 2]  # 选择中间元素作为基准
    left = [x for x in arr if x < pivot]  # 小于基准的元素
    middle = [x for x in arr if x == pivot]  # 等于基准的元素
    right = [x for x in arr if x > pivot]  # 大于基准的元素

    return quick_sort(left) + middle + quick_sort(right)  # 递归排序并合并

# 测试代码
arr = [10, 7, 8, 9, 1, 5]
sorted_arr = quick_sort(arr)
print("排序后的数组:", sorted_arr)

🔹 运行结果

1
排序后的数组: [1, 5, 7, 8, 9, 10]

🔹 时间复杂度

  • 最佳情况：( O(n \log n) )
  • 最差情况（已排序数组）：( O(n^2) )
  • 平均情况：( O(n \log n) )

🔹 空间复杂度

  • ( O(\log n) )（递归栈空间）
  • 最差情况可能达到 ( O(n) )（当每次都选到最小/最大元素作为基准）

✅ 快速排序通常比归并排序更快，因为它不需要额外的合并步骤！ 🚀

堆排序

总结

License

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。