线代

行列式的概念

排列

不同的元素排成一列，就称之为这n个元素的n级排列，简称为排列，记为$j_{1}j_{2}j_{3}…j_{n}$

逆序

在一个n级排列$j_1j_2\cdots j_s\cdots j_t\cdots j_n$中，数$j_s$与$j_t$满足$j_s>j_t$（“大前小后”），则$j_s$与$j_t$构成一个逆序。
一个排列中逆序的总数称为此排列的逆序数，记为$\tau(j_1j_2\cdots j_n)$。

如：一个6级排列231645的逆序数为：$\tau(231645)=1 + 1+0 + 2+0 = 4$
123456（自然排列）的$\tau(123456)=0 + 0+0 + 0+0 = 0$

对换

排列$j_1j_2\cdots j_n$中，交换任意两个数的位置，其余不变，则称对排列作了一次对换。

奇排列，偶排列

若排列$j_1j_2\cdots j_n$的$\tau(j_1j_2\cdots j_n) =$奇数，则称$j_1j_2\cdots j_n$为奇排列

如：$\tau(231645)=4$，则231645为偶排列.
$\tau(123\cdots n)=0$，则$(123\cdots n)$为偶排列.
$\tau(n,n - 1,\cdots,3,2,1)=\frac{n(n - 1)}{2}$，其奇偶性与n有关.
$\tau(132)=1$，则132为奇排列.
$\tau(231)=2$，则231为偶排列.

对换一次，奇偶性改变

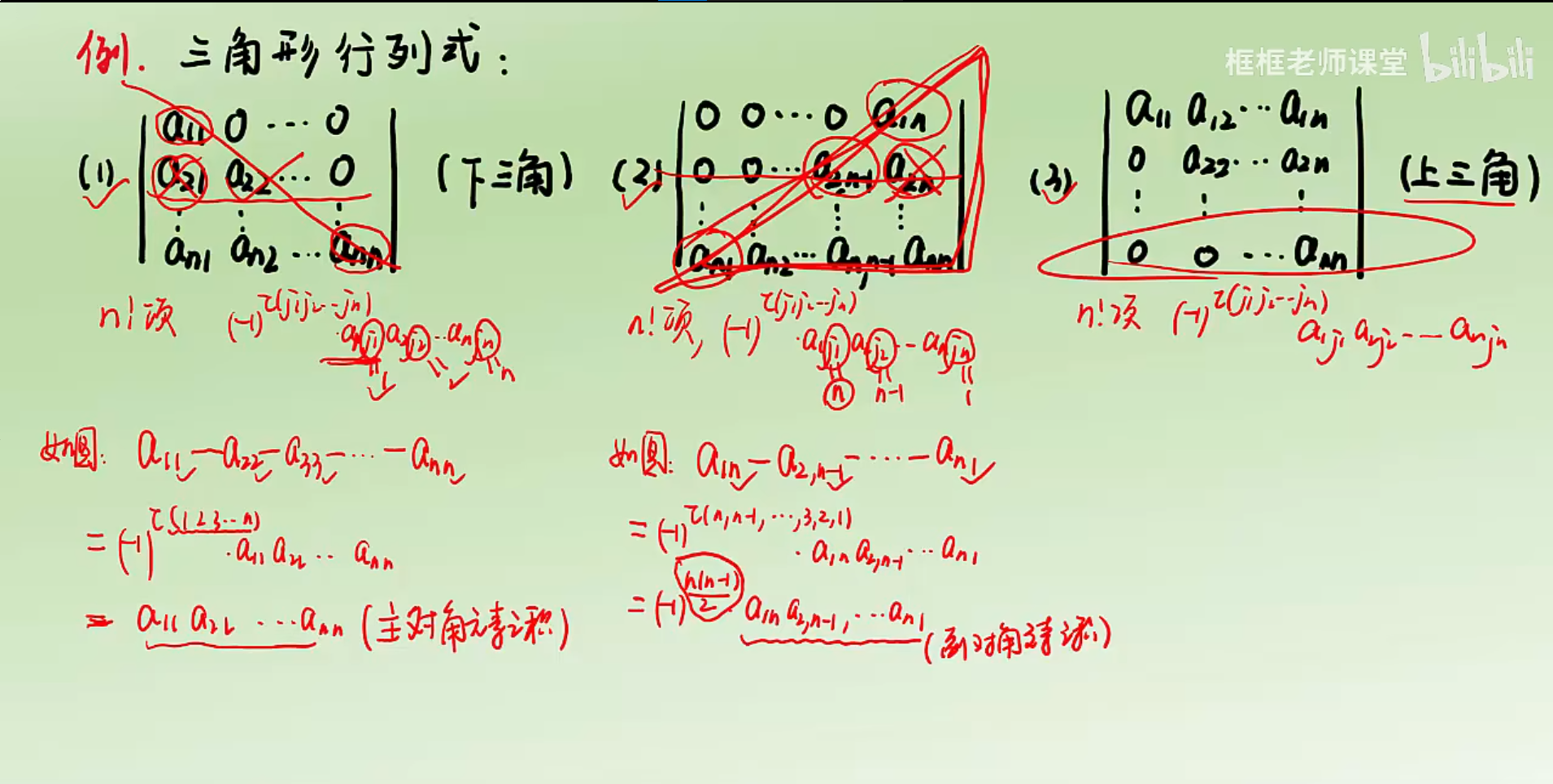
对角线法则

n阶行列式定义

三角形的行列式

行列式的性质

1.行列式的行和列互换，行列式的值不变

2.行列式的某两行（两列）互换，值反号

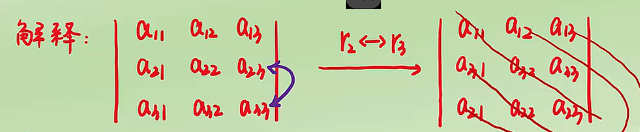
若行列式有两行或两列相同，则行列式为0

3.行列式的某行（列）可以提取公因子

若行列式有行全为0则行列式的值为0

4.若行列式有两行(列)成比例，则为0

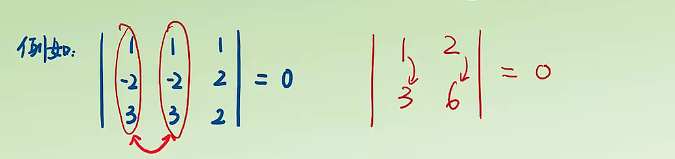
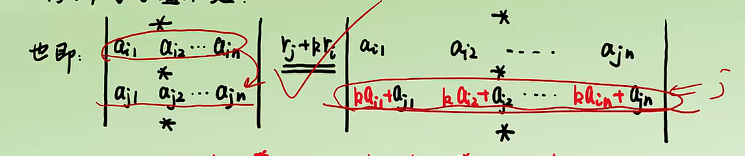
5.若行列式某行（列）元素均为两数之和，则行列式可拆分为两个简单的行列式值和

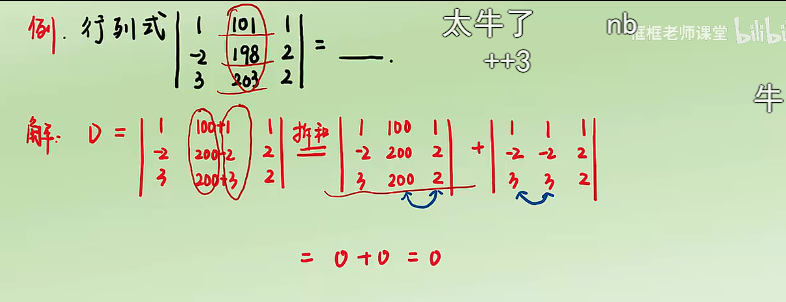
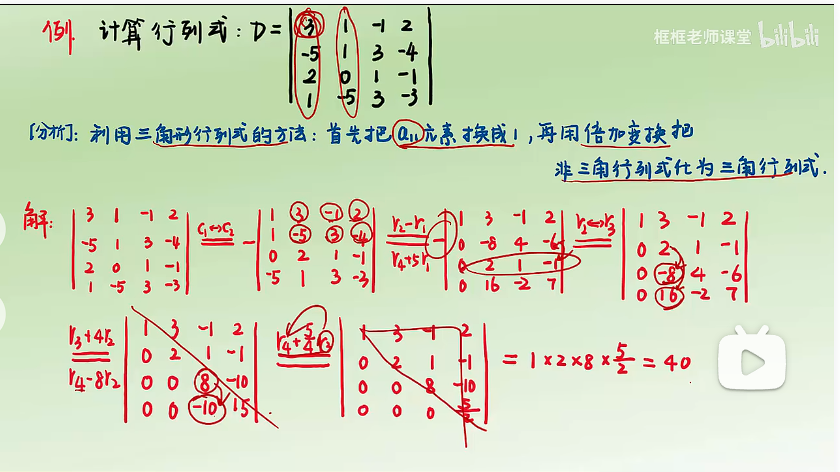
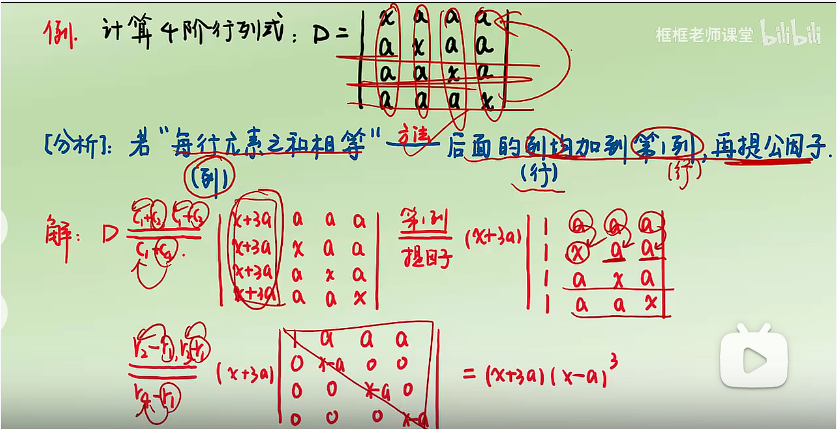
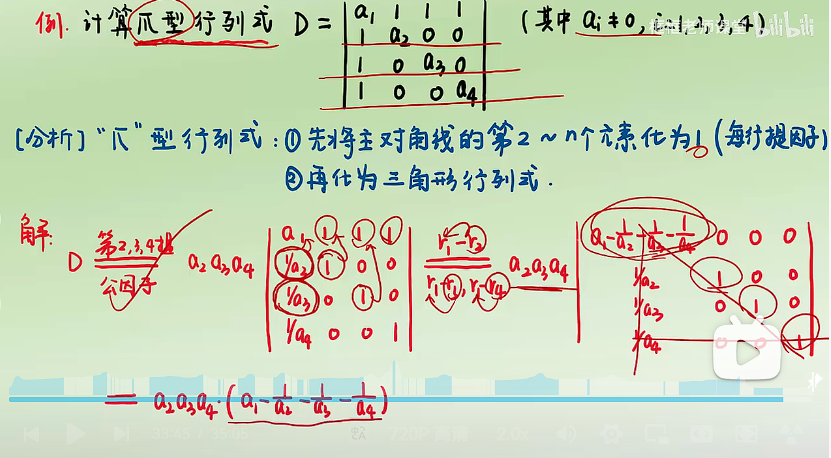
习题

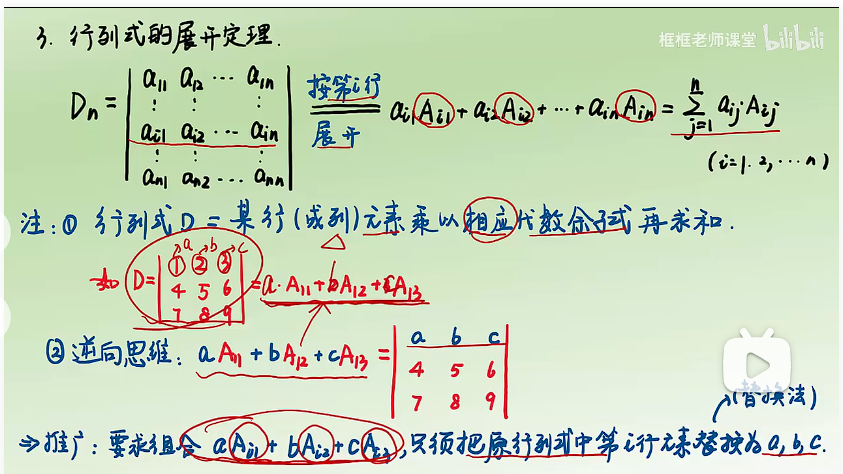
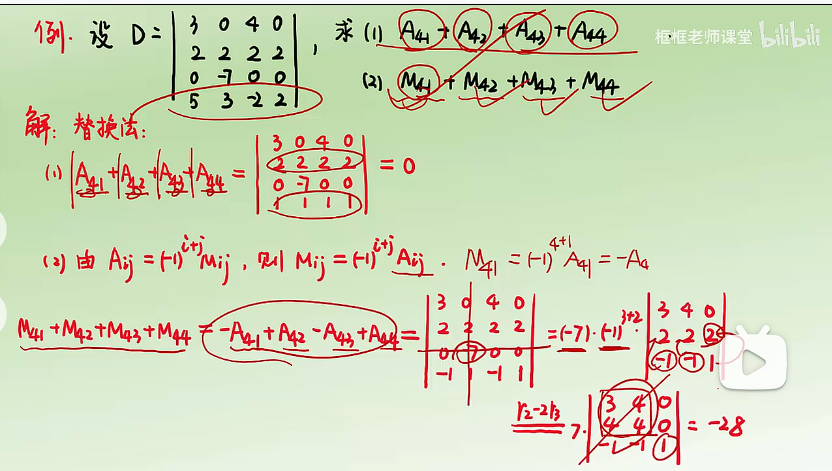
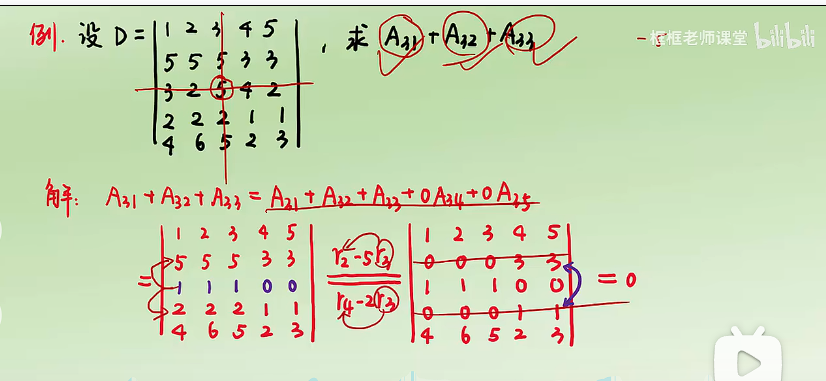
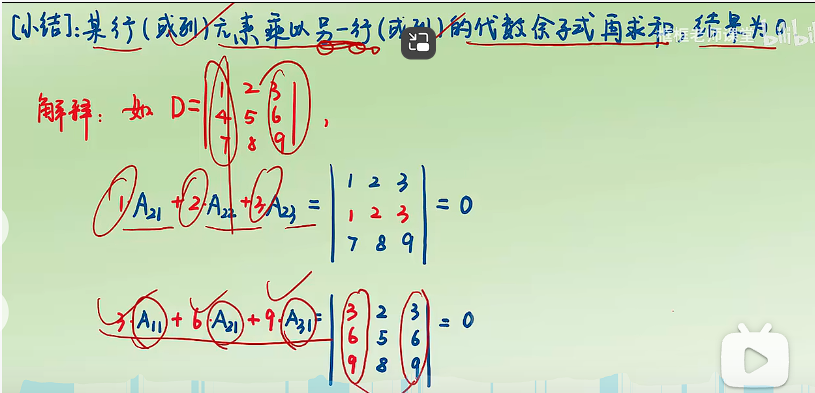
行列式展开定理